rethinking the absolute towers
THE ABSOLUTE TOWERS
OFFICE BUILDINGS
MISSISSAUGA, CANADA
Architects: MAD Architects
Year: 2012
THE ABSOLUTE TOWERS ARE A PAIR OF OFFICE BUILDINGS IN CANADA THAT USE PARAMETRIC DESIGN TO CREATE A TWISTING PATTERN.
1. HOW CAN WE MAKE THIS BETTER?
- I CAME UP WITH AN IDEA TO ADD VERTICAL SHADING DEVICES TO THIS BUILDING, THAT TWIST AROUND IT DIFFERENTLY THAT THE EXISTING TWIST OF THE FLOOR PLATES. IN THEORY THIS WOULD CREATE AN ADDITIONAL LEVEL OF OF GEOMETRY AND AESTHETICS TO THE BUILDING. I FIRST TESTED THIS IDEA WITHIN CHAT GPT.
AFTER TRYING A FEW MORE TIMES, I WAS ABLE TO GET AN IMAGE THAT ATLEAST VISUALIZED THE IDEA OF VERTICLE MULLIONS THAT TWIST AROUND THE BUILDING AND MAKE THE VISUAL EVEN MORE WAVY AND ENTRANCING. HOWEVER IN ORDER TO CREATE THIS GEOMETRY, WE WOULD HAVE TO UNDERSTAND THE ORIGINAL DESIGN FIRST.
THE TWO TOWERS ARE CREATED FROM THE SAME PARAMETRIC DESIGN, WITH CERTAIN PARAMETERS CHANGED, SO DESIGNING ONE OF THESE TOWERS SHOULD BE ABLE TO ACCOUNT FOR THEM BOTH.
EACH FLOOR IS A IRREGULAR OVAL - LIKE SHAPE THAT COULD BE CONSTRUCTED FROM AN INTERPOLATED CURVE.
EACH FLOOR IS A COPY OF THE ONE BELOW IT, ONLY ROTATED A CERTAIN AMOUNT OF CHANGING DEGREES. AS YOU CAN SEE THE FLOOR ROTATE MORE DRAMATICALLY TOWARDS THE MIDDLE.
2. PARAMETRIC MODELING
A. THE SCRIPT FIRST CONSTRUCTS 5 CONTROL POINTS WHICH IT USES TO CREATE AN INTERPOLATED CURVE.
B. THE PROJECT THEN ARRAYS THESE CURVES UPWARD 50 TIMES, FOR 50 FLOORS. EACH CURVE IS SPACED 10 FEET APART.
C. WE NEED TO ROTATE THE FLOORS IN A NON CONSISTENT WAY SO THAT THE DEGREE OF ROTATION IS CHANGING, CREATING THE WAVE AFFECT. WE CAN DO THIS BY USING A GRAPH MAPER, WHICH WILL ROTATE THE FLOORS ALONG WITH THE CURVE OF THE GRAPH. THIS GRAPH IS CONTROLLED BY A DOMAIN WHICH HERE REPRESENTS THE MINIMUM 0 AND MAXIMUM 360 DEGREES OF ROTATION. THE RANGE REPRESENTS THE AMOUNT OF FLOORS, WITH A SUBTRACTION OF 1 TO MAKE UP FOR GRASSHOPPER COUNTING ZERO AS 1 IN A LIST.
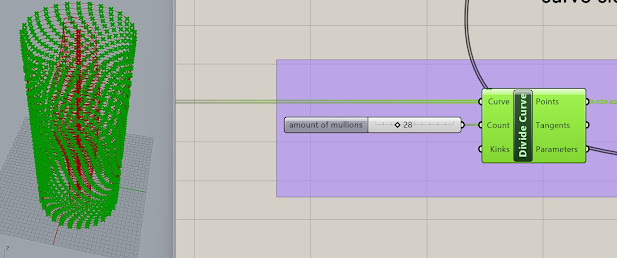
E. IN ORDER TO CREATE A NEW MULLION SYSTEM THAT TWISTS AROUND THE BUILDING, I WILL START BY CREATE A SERIES OF REGULAR CIRCLES, WHICH ARE ARRAYED UP ALONG WITH EACH FLOOR.
G. I CAN THEN SUBDIVIDE THESE CIRCLES TO GET NEW POINTS WHICH REFLECT THE NEW WAVY PATTERN WE ESTABLISHED WITH THE GRAPH AND ROTATION.
H. I CAN THEN USE A CURVE CLOSEST POINT COMMAND THAT WILL TAKE THE POINTS ON THE CIRCLE AND SELECT THE CLOSEST POINT ON THE EXISTING CURVES. THESE NEW POINTS WILL STILL HAVE THE WAVY PATTERN, BUT WILL BE NO REFLECTED ONTO THE EXISTING TOWER VOLUME.
I. HERE YOU CAN SEE THOSE NEW POINTS REFLECTED ON THE EXISTING VOLUME.
J. WE CAN THEN USE POLYLINES TO CONNECT THESE NEW POINTS WHICH TWIST AROUND THE BUILDING. HOWEVER, WE FIRST NEED TO FLIP THE MATRIX OF THE DATA POINTS SO THAT EACH DATA SET IS NO LONGER GROUPED BY FLOOR BUT IS INSTEAD GROUPED BY DATA POINT.
K. THIS SHOWS HOW THE DATA STRUCTURE IS NOW FLIPPED, WITH POINTS RUNNING FROM 0 TO 49 FOR EACH OF THE FLOORS. THIS WAY, A POLYLINE WILL RUN FROM THE FIRST FLOOR POINT , THROUGH THE FIRST POINT ON EVERY FLOOR, AND END WITH THE FIRST POINT OF THE TOP FLOOR.
L. WE CAN THEN USE A POLIGON COMMAND TO ADD A POLYGON AT EACH DATA POINT ON THE SKIN. WE CAN THEN LOFT THOSE POLYGONS TO CREATE MULLIONS THAT HAVE A SET THICKNESS.
M. WE CAN ALSO CREATE THE FLOOR PLATES BY GOING BACK TO THE ORIGINAL BUILDING FLOOR CURVES, EXTRUDING THEM, AND CAPING THEM.
N. WE CAN ALSO CREATE THE GLASS SKIN BY SIMPLY LOFTING ALL OF THE EXISTING FLOOR LINES TOGETHER.
O. HERE WE SEE THE GAUSIAN ANALYSIS OF THE SHOWS SOME OF THE SHARPER EDGES.
THE SURFACE AREA IS 120,283 SQ FT.
P. THE FINAL PRODUCT SHOWS THE NEW TWISTING PATTERN OF THE MULLIONS, WHICH CAN BE ADJUSTED TO BE MORE DENSE OR FAR APART.
WORKS CITED:
Comments
Post a Comment